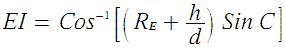Antenna Look Angles : Determination Of The Azimuth And Elevation Angles

Antenna look angles

Determination of the Azimuth and Elevation angles (Look Angles)

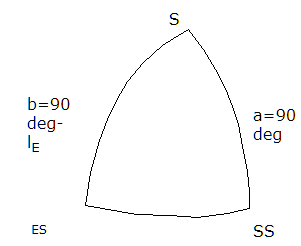
Figure-1 shows spherical triangle bounded by points N, ES, and SS.

Here ES denotes the earth station. The point s denotes the satellite in geostationary orbit, and point SS the sub satellite point. To solve this triangle we have to use Napier's rules. By solving we get following results.

Let l_E represents the latitude of the earth station, f_E represents the longitude and of the earth station, f_S the longitude of sub satellite point, and observing the sign convention stated previously, the angle B is given by

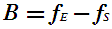
B can not exceed a theoretical limit of 81.3° , set by horizon. Napier's rules can then be used to show

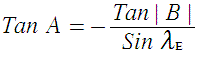
Once angle A is determined, the azimuth angle A_Z can be found. Four situations must be considered, the results for which can be summarized as follows:

(a) l_E<0;B<0:A_Z= A

(a) l_E<0;B>0:A_Z= 360°-A

(a) l_E>0;B<0:A_Z= 180°+A

(a) l_E>0;B>0:A_Z= 180°-A

These do not take into account the case when the earth station is on the equator. Obviously, when the sub-satellite, the elevation is 90° and Azimuth is irrelevant. When the west (B >0 ), the azimuth is 270°.

To find the range and elevation, it is necessary first to find side c of the quadrantal spherical triangle, and then use this in the plane triangle shown in fig. side c is obtained using the rule.

The equatorial radius R_E= 6378.14 km, and geostationary height h = 35,786 km. Because of the flattening of the earth at the poles, the radius R varies with latitude. An equation that gives R to a close approximation is

Here R_E is the earth's equatorial radius and R is the radius at the earth station.

The plane triangle shown in fig-2 can be solved using the plane trigonometry. Applying the cosine rule gives the distance d as.

The elevation angle is denoted by EI deg in fig . Application of the sine rule to the plane triangle gives

Example Problem